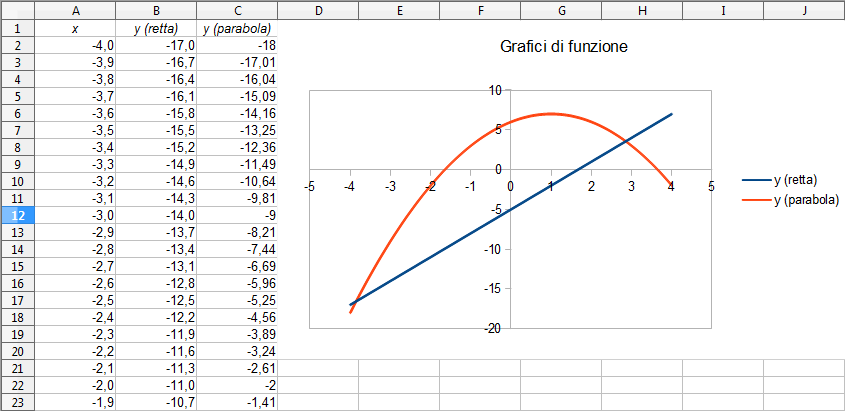
Grafico di funzioni con il foglio di calcolo
Si vogliono graficare sul piano cartesiano una retta e una parabola con il foglio di calcolo (Openoffice Calc oppure Microsoft Excel), prima rappresentandole per punti e poi utilizzando le funzioni grafiche del programma.
Preparazione della colonna con i valori delle ascisse.
Nella prima colonna del foglio di calcolo elencheremo i valori dell'asse x.
Iniziamo quindi scrivendo una x (centrata ed in corsivo) nella cella A1.
Supponiamo ora di voler rappresentare l'intervallo compreso tra i valori -4 e +4 e che la distanza tra punti consecutivi sia di 0,1. Si può fare in due modi:
- Primo metodo:
- Scrivi i primi due valori nelle prime due caselle della colonna (-4 nella casella A2 e -3,9 nella casella A3):
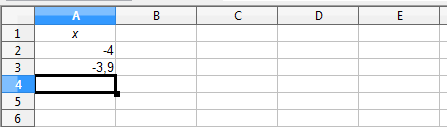
- Seleziona le due caselle:
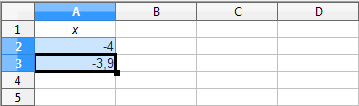
- Posiziona il puntatore del mouse nell'angolo in basso a destra della selezione (il puntatore assumerà l'aspetto di una piccola croce):

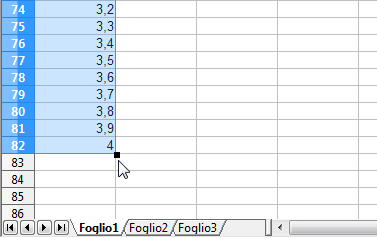
- Trascina verso il basso fin quando vedrai comparire il valore 4:
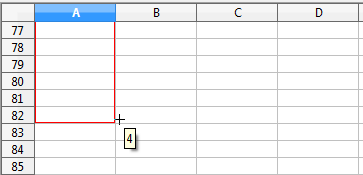
- Scrivi i primi due valori nelle prime due caselle della colonna (-4 nella casella A2 e -3,9 nella casella A3):
- Secondo metodo:
- Scrivi -4 nella casella A2 e la formula =A2+0,1 nella casella A3:
 Dopo aver premuto INVIO il programma effettuerà il calcolo della formula, quindi nella casella A3 comparirà il valore -3,9, come nel metodo precedente. Ricordati, però, che questa volta la casella A3 in realtà contiene una formula, non un valore.
Dopo aver premuto INVIO il programma effettuerà il calcolo della formula, quindi nella casella A3 comparirà il valore -3,9, come nel metodo precedente. Ricordati, però, che questa volta la casella A3 in realtà contiene una formula, non un valore. - Ora seleziona solo la casella A3 e posiziona il puntatore del mouse nel suo angolo in basso a destra:

- Trascina verso il basso. Questa volta, durante il trascinamento, non compare l'etichetta gialla con il valore raggiunto (perché, dal momento che stai copiando una formula, questa verrà calcolata solo al termine dell'operazione). Devi quindi procedere "per tentativi": trascina fino ad un certo punto, quindi rilascia il pulsante del mouse e verifica il valore a cui sei arrivato:
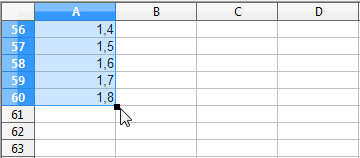 Se hai superato il valore al quale dovevi arrivare (nel nostro esempio 4), cancella i valori in eccesso. Se, come in figura, ti sei fermato troppo presto, riprendi l'angolo in basso a destra della cella a cui ti sei fermato e trascina di nuovo.
Se hai superato il valore al quale dovevi arrivare (nel nostro esempio 4), cancella i valori in eccesso. Se, come in figura, ti sei fermato troppo presto, riprendi l'angolo in basso a destra della cella a cui ti sei fermato e trascina di nuovo.
- Scrivi -4 nella casella A2 e la formula =A2+0,1 nella casella A3:
Per capire la differenza tra i due metodi, prova ad utilizzare il primo per riempire la colonna A ed il secondo per riempire la colonna B (a partire dalle celle A2 e B2, supponendo di lasciare le celle A1 e B1 per l'intestazione). Poi prova a modificare il valore di partenza di entrambe le colonne, scrivendo ad esempio -2 sia nella cella A2 che nella cella B2. Che cosa osservi?
Avrai notato che il secondo metodo, quello che utilizza la formula, permette di modificare l'intera sequenza di valori semplicemente cambiando il primo.
Avrai notato anche che la precisione con cui sono rappresentati i valori non è uniforme: il programma elimina la cifra decimale quando questa è uguale a zero; inoltre, utilizzando il secondo metodo, alla cella A42 compare, al posto del valore 0, un valore molto piccolo ma non nullo, causato da problemi nella rappresentazione interna dei numeri utilizzata dal programma.
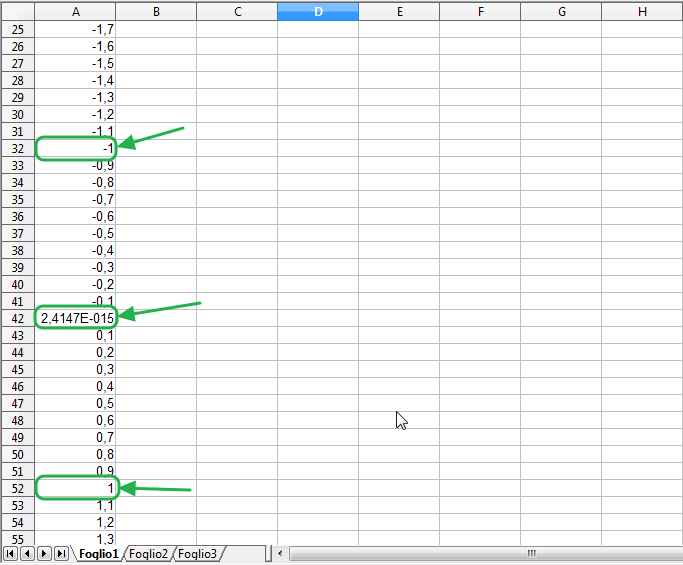
Per ottenere maggiore uniformità nella rappresentazione dei valori:
- seleziona la colonna cliccando sulla lettera A posta in testa ad essa;

- clicca con il tasto destro sulla selezione e, nel menu contestuale, scegli "Formatta celle...";

- nella finestra che si apre, nella scheda "Numeri", scrivi 1 nella casella "Posizioni decimali":
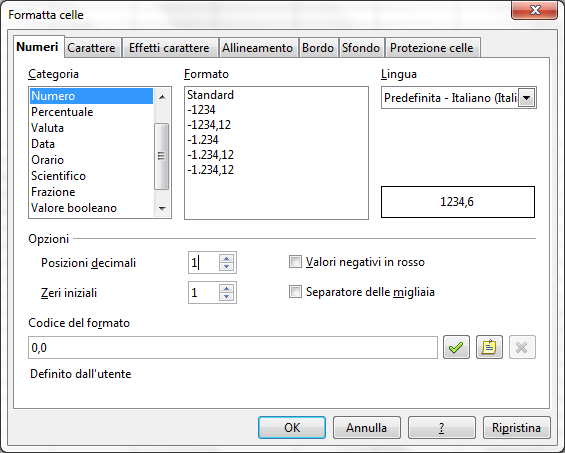
A questo punto, verifica che i problemi che avevi osservato sono stati risolti: tutti i valori sono rappresentati con una precisione di una cifra decimale.
- Primo metodo:
Calcolo dei punti della retta.
Vogliamo rappresentare il grafico della retta di equazione y = 3x - 5 .
Innanzitutto inseriamo un'intestazione anche alla colonna B: nella cella B1 scrivi y (retta) .
Come abbiamo già detto, la retta viene tracciata punto per punto. Quindi, in corrispondenza di ogni valore dell'ascissa nella colonna A dobbiamo calcolare il valore dell'ordinata. Per fare ciò, basta sostituire il valore della x nell'equazione della retta e calcolare y.
Inizia con il primo punto, scrivendo la formula
=3*A2-5nella casella B2:
Quindi premi INVIO. Il programma calcolerà il risultato della formula, ossia il valore di y corrispondente ad x = - 4 :

Ora, poiché nella formula hai utilizzato un riferimento relativo, copiando la formula nelle celle sottostanti, essa verrà "adattata" automaticamente per fare riferimento, da ogni cella della colonna B, alla cella posta sulla stessa riga della colonna A.
Dopo aver selezionato la cella B2, trascina verso il basso il suo angolo inferiore fino alla cella B82:
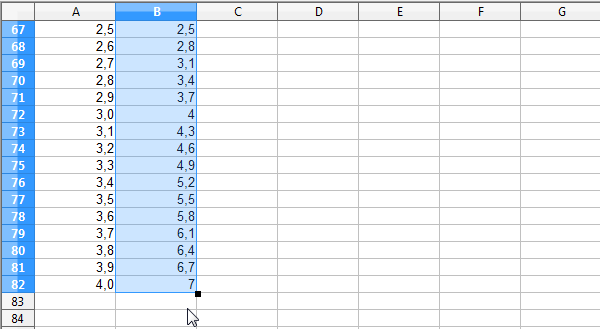
Anche in questo caso, come hai fatto per la colonna A, formatta l'intera colonna per rappresentare i valori con una precisione alla prima cifra decimale.
Creazione del grafico della retta.
Per tracciare il grafico della retta, seleziona le due colonne A e B e clicca sul pulsante "Grafico":
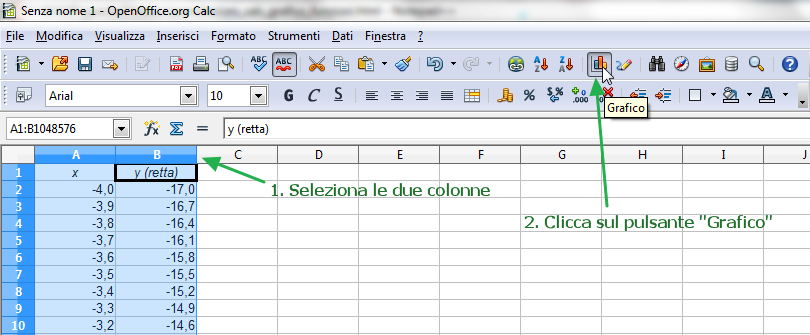
Se il pulsante "Grafico" non è presente, dopo aver selezionato le due colonne, clicca sulla voce "Grafico..." del menu "Inserisci":

Si apre la finestra "Creazione guidata grafico":
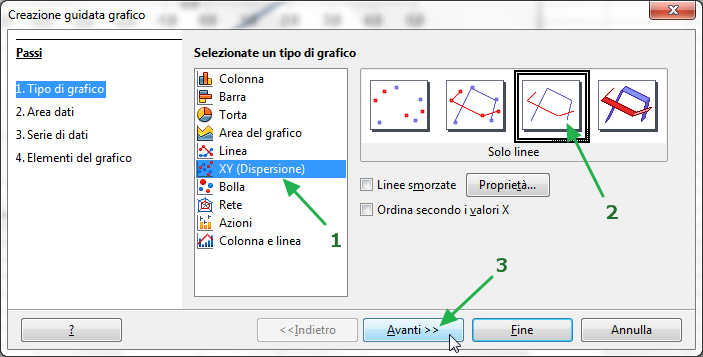
Effettua le selezioni indicate in figura.
Continua a cliccare il pulsante "Avanti" fino ad arrivare al passo 4. Qui, nella casella "Titolo" scrivi "Grafici di funzione" e poi togli la spunta alla casella "Asse Y" nella sezione "Mostra le griglie" (e nota l'effetto di questa deselezione sul grafico):

Dopo aver cliccato su "Fine" potrai ammirare il grafico ottenuto:
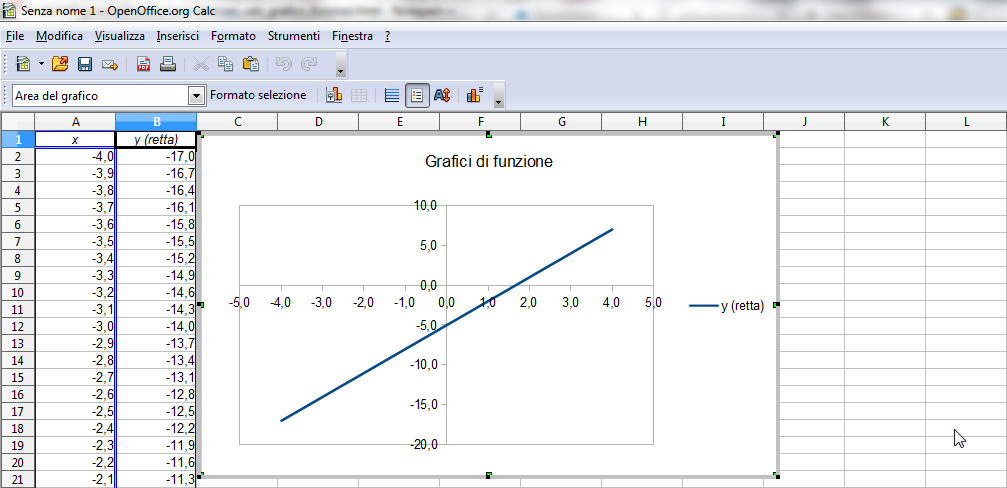
Ora modifichiamo alcune impostazioni del grafico:
Etichette dell'asse x : clicca con il destro sull'asse x e seleziona "Formato asse...";

nella finestra che si apre, vai alla scheda "Numeri" e deseleziona la casella "Formato sorgente", che indica che sulle etichette degli assi i valori sono rappresentati con le stesse impostazioni scelte per le celle del foglio di calcolo (ricordi che hai scelto di proposito di visualizzare una cifra decimale?);
per finire, inserisci il valore 0 nella casella "Posizioni decimali":
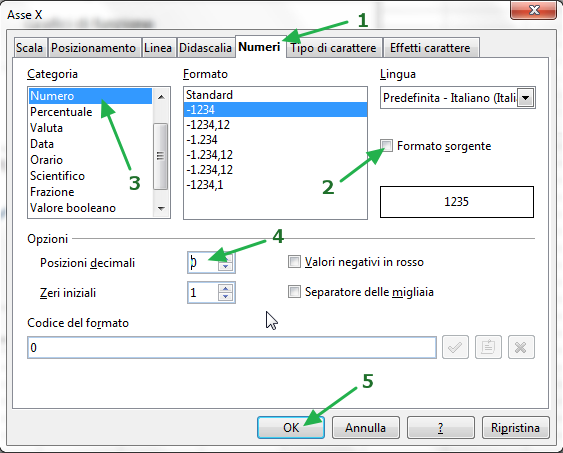
Etichette dell'asse y : ripeti il procedimento appena svolto per l'altro asse.
A questo punto, l'aspetto del grafico è il seguente:

Prima di passare al punto successivo, riposiziona il grafico trascinandolo dove preferisci.
Calcolo dei punti della parabola.
Vogliamo ora rappresentare il grafico della parabola di equazione y = - x^2 + 2 x + 6 .
Innanzitutto inseriamo un'intestazione alla colonna C: nella cella C1 scrivi y (parabola) .
Come abbiamo fatto per la retta, anche per la parabola tracceremo l'andamento punto per punto. Quindi, in corrispondenza di ogni valore dell'ascissa nella colonna A dobbiamo calcolare il valore dell'ordinata. Per fare ciò, basta sostituire il valore della x nell'equazione della parabola e calcolare y.
Inizia con il primo punto, scrivendo la formula
=-(A2^2)+2*A2+6nella casella C2 (le parentesi sono necessarie poiché il segno - ha la precedenza rispetto al calcolo della potenza).
Quindi premi INVIO. Il programma calcolerà il risultato della formula, ossia il valore di y corrispondente ad x = - 4 . A questo punto copia la formula su tutta la colonna trascinando la casella verso il basso, così come hai fatto in precedenza per la retta.

Per assicurarti di non aver commesso errori, verifica che i primi valori corrispondano a quelli della figura precedente.
Aggiunta del grafico della parabola.
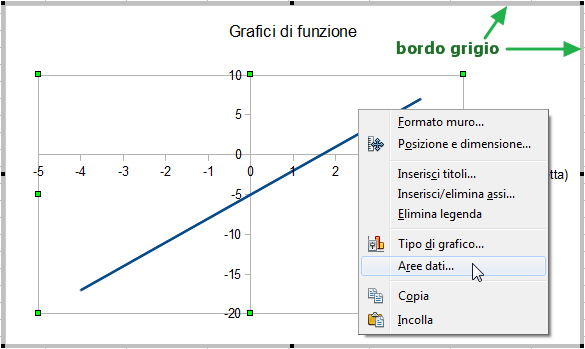
Per aggiungere al grafico già creato in precedenza la curva corrispondente alla parabola, seleziona il grafico facendo doppio clic su di esso. La cornice del grafico dovrebbe diventare di colore grigio.
Clicca con il destro sul grafico e, dal menu contestuale, seleziona "Aree dati...":
Nella finestra che si apre, all'interno della scheda "Serie dati", sono elencate tutte le serie di dati che sono rappresentate sul grafico. Nel nostro caso, per ora è presente solo la retta (nell'elenco "Serie di dati", sulla sinistra, c'è la sola voce "y (retta)"). Nel riquadro "Aree dati", per ogni serie di dati sono elencate le aree in cui si trovano il nome della serie, i suoi valori X e i suoi valori Y.
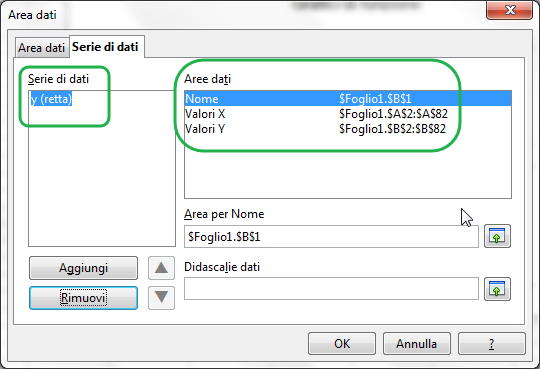
Il formato (o codice) in cui sono espresse le aree dati dovrebbe essere autoesplicativo:
$Foglio1.$B$1significa: "cella B1 del Foglio1" (in cui infatti si trova il nome della serie di dati, nel caso specifico "y (retta)");$Foglio1.$A$2:$A$82significa: "l'intervallo di celle comprese tra la cella A2 e la cella A82 del Foglio1" (in cui infatti si trovano i valori delle ascisse della serie dati);$Foglio1.$B$2:$B$82significa: "l'intervallo di celle comprese tra la cella B2 e la cella B82 del Foglio1" (in cui infatti si trovano i valori delle ordinate della serie dati).
Una volta che avrai capito questo modo di esprimere le aree dati, sarai in grado di aggiungere un'altra serie di dati, corrispondente alla parabola, esprimendo le sue aree dati nello stesso modo.
Per aggiungere un'altra serie dati, clicca sul pulsante "Aggiungi".
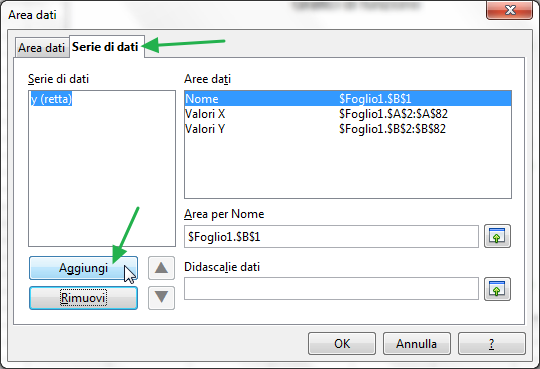
Come puoi notare, è stata aggiunta un'altra serie dati all'elenco, dal nome provvisorio "Serie senza nome". Il nome può essere inserito digitando direttamente nella casella "Area per nome" il codice che rappresenta la cella C1, ossia
$Foglio1.$C$1. Oppure, per evitare errori di digitazione, si può cliccare sul piccolo quadratino che si trova alla destra della casella.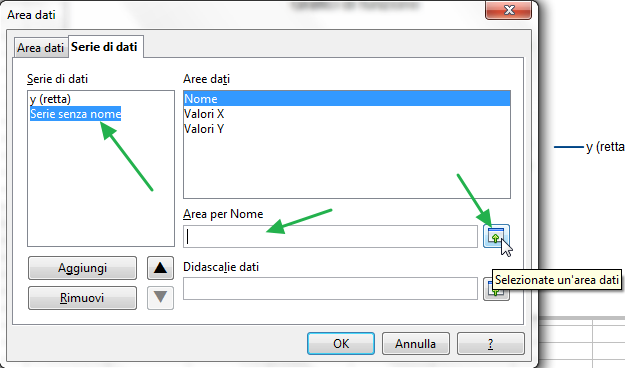
Si apre una (mini)finestra in cui, cliccando sulla cella C1, verrà scritto in automatico il codice ad essa corrispondente.
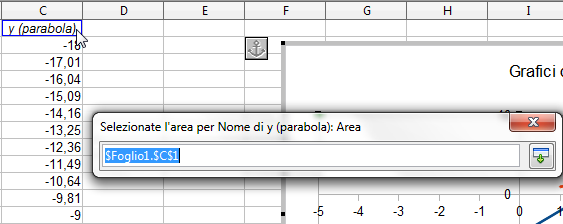
La finestra scompare immediatamente e il codice si ritrova nella casella "Area per nome", come desiderato:
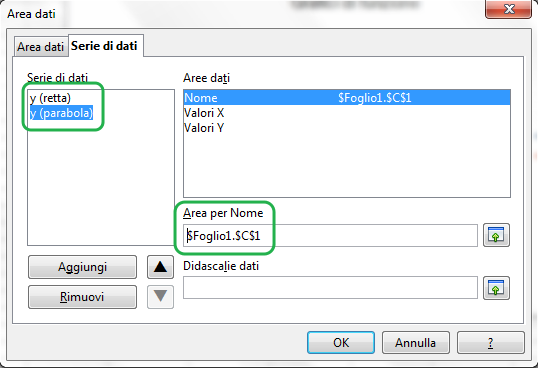
Notare inoltre che nell'elenco delle serie dati ora la serie compare con il nome "y (parabola)", preso appunto dalla cella C1.
In maniera analoga occorre ora specificare i valori X e i valori Y della serie. Poiché i valori X sono gli stessi della serie "y (retta)", sarà sufficiente copiare e incollare il codice
$Foglio1.$A$2:$A$82.Copia:
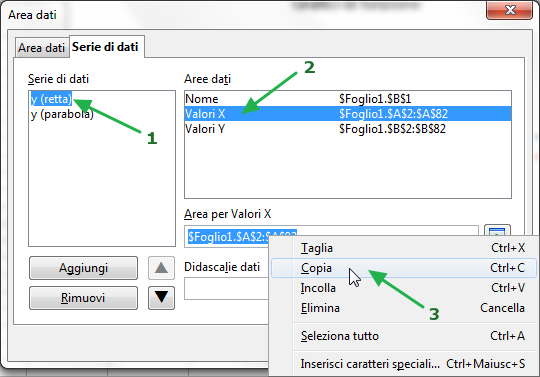
Incolla:

Per quanto riguarda i valori Y della parabola, la nostra area dati saranno le celle comprese tra la riga 2 e la riga 82 della colonna C, ossia il codice
$Foglio1.$C$2:$C$82.Anche in questo caso, puoi inserire il codice digitandolo nella casella "Area per valori Y"; oppure, per non rischiare errori di digitazione, puoi incollare il codice già incollato al passo precedente
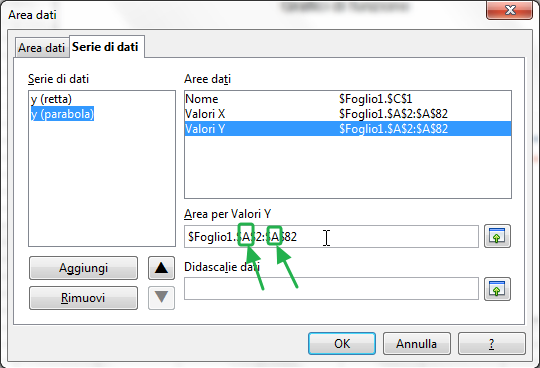
e rimpiazzare le due lettere A che vi compaiono (evidenziate nella figura) con delle C:

Ed ecco il risultato finale: sullo stesso piano cartesiano, i due grafici di una retta e di una parabola: